Houdini VEX sink
· Houdini MOC · Houdini VEX · Houdini VEX reference · #note/sink · #code/vex
TOC
Data types
| int | Integer values |
| float | Floating point scalar values |
| vector2 | Two floating point values |
| vector | Three floating point values |
| vector4 | Four floating point values. |
| array | A list of values |
| struct | A fixed set of named values (class) |
| matrix2 | { {1,0}, {0,1} } |
| matrix3 | { {1,0,0}, {0,1,0}, {0,0,1} } |
| matrix | { {1,0,0,0}, {0,1,0,0}, {0,0,1,0}, {0,0,0,1} } |
| string | A string of characters |
| dict | A dictionary mapping strings to other VEX data types |
| bsdf | A bidirectional scattering distribution function |
Specifying VEX Data Types
The following characters are used to cast to the corresponding data type.
float f@name // Floating point scalar values.
vector2 u@name // Two floating point values. Could be used to store 2D positions.
vector3 v@name // Three floating point values. Usually positions, directions, normals, UVW or colors.
vector4 p@name // Four floating point values. Usually rotation quaternions, or color and alpha (RGBA).
int i@name // Integer values (VEX uses 32 bit integers).
matrix2 2@name // Four floating point values representing a 2D rotation matrix.
matrix3 3@name // Nine floating point values representing a 3D rotation matrix or 2D transform matrix.
matrix 4@name // Sixteen floating point values representing a 3D transform matrix.
string s@name // A string of characters.
Type casting
int a, b;
float c;
c = (float)a / (float)b; // float(a) is unnecessary
// type cast a function
float n;
n = noise(noise(P));
n = noise(vector(noise(P)));
Operator type interactions
1/100 results in integer, 1/100.0 results in float.
See [[#Operator type interactions]]
float * int = float
int * float = int
vector * scalar = vector
v2 * v4 = v4
**Important!!!**
The “missing” component(s) on the smaller vector are filled in as {0.0, 0.0, 0.0, 1.0}
Vector
@v = {1, 1, 1}
v@v = set(x, y, z)
Dictionary
reading motion clip clipinfo (detail attribute) range value
dict clipinfo = detail("op:../motionclip", "clipinfo");
printf("clipinfo=%d", clipinfo); // this will help find the datatypes inside the dictionary
vector2 crange = getcomp(clipinfo, "range"); // get the value of "range" key
printf("range=%d", crange); // just checking the value
adddetailattrib(0, "clip_range_end", crange[1]); //set the value to current geo detail
Operators
Dot operator
// vector
v = set(v.x, v.y, v.z);
v = set(v.r, v.g, v.b);
// vector2
v2 = set(v2.x, v2.y);
v2 = set(v2.u, v2.v);
// vector4 forth element
f = v4.a;
f = v4.w;
// matricies
m[0][0] = m.xx;
m[2][2] = m.zz;
m[3][0] = m.ax;
//components
v.zyx = set(v.z, v.y, v.x);
v4.bgab = set(v4.b, v4.g, v4.a, v4.b);
Comparisons
The logical (&&, ||, and !) and bitwise (& |, ^, and ~) operators are only defined for integers
All bool operations are casted to integers!
Pragmas
#pragma opname noise_surf
#pragma oplabel "Noisy Surface"
#pragma label clr "Color"
#pragma label frequency "Frequency"
#pragma hint clr color
#pragma range frequency 0.1 10
surface noise_surf(vector clr = {1,1,1}; float frequency = 1; export vector nml = {0,0,0})
{
Cf = clr * (float(noise(frequency * P)) + 0.5) * diffuse(normalize(N));
nml = normalize(N)*0.5 + 0.5;
}
Channel Shortcut Syntax
This is used to hint at the data type of auto generated wrangle parameters.
ch('flt1'); // Float
chf('flt2'); // Float
chi('int'); // Integer
chv('vecparm'); // Vector 3
chp('quat'); // Vector 4 / Quaternion
ch3('m3'); // 3x3 Matrix
ch4('m4'); // 4x4 Matrix
chs('str'); // String
chramp('r', x); // Spline Ramp
vector(chramp('c', x)); // RGB Ramp
Remapping attribs
parm*=rand(@id+38+ch("seed"));
//random number, linear spread
parm=fit01(rand(@id+31+ch("seed")),ch("min"),ch("max"));
//particle age -> Ease in - Ease out
parm*=smooth(ch("start"), ch("end"),@nage);
//parameter change in a certain time range
parm=fit(@Frame, ch("start"), ch("end"), ch("start_value"), ch("end_value"));
//connect params
parm=fit(@P.y, ch("low"), ch("high"), ch("low_value"), ch("high_value"));
//param from age by multiplier
parm*=chramp("parm",@nage);
//param from a particle speed
parm=fit(length(@v),ch("speedmin"),ch("speedmax"), ch("valuemin"), ch("valuemax"));
Orientation
// orient your points towards your velocity vector:
@orient = dihedral({0,0,1} ,@v);
Calculate the orient attribute from normals:
matrix3 m = dihedral({0,1,1},@N);
@orient = quaternion(m);
Calculate the heading and up vectors from the orient attribute:
matrix3 rr = qconvert(@orient);
v@up = set(rr.yx,rr.yy,rr.yz);
v@heading = set(rr.zx,rr.zy,rr.zz);
Sampling functions
Random Directed Vectors
Source
Sample Direction Uniform
Sample Direction Uniform
This is a great way of getting “random” vectors but you need the vectors to be “clamped” to a certain range of “spread”.
To illustrate this, we’ll use a buncha points on a grid and “shoot” (aka move) them out “randomly” using sample functions.
vector2 u = rand(@ptnum);
@P = sample_direction_uniform(u);
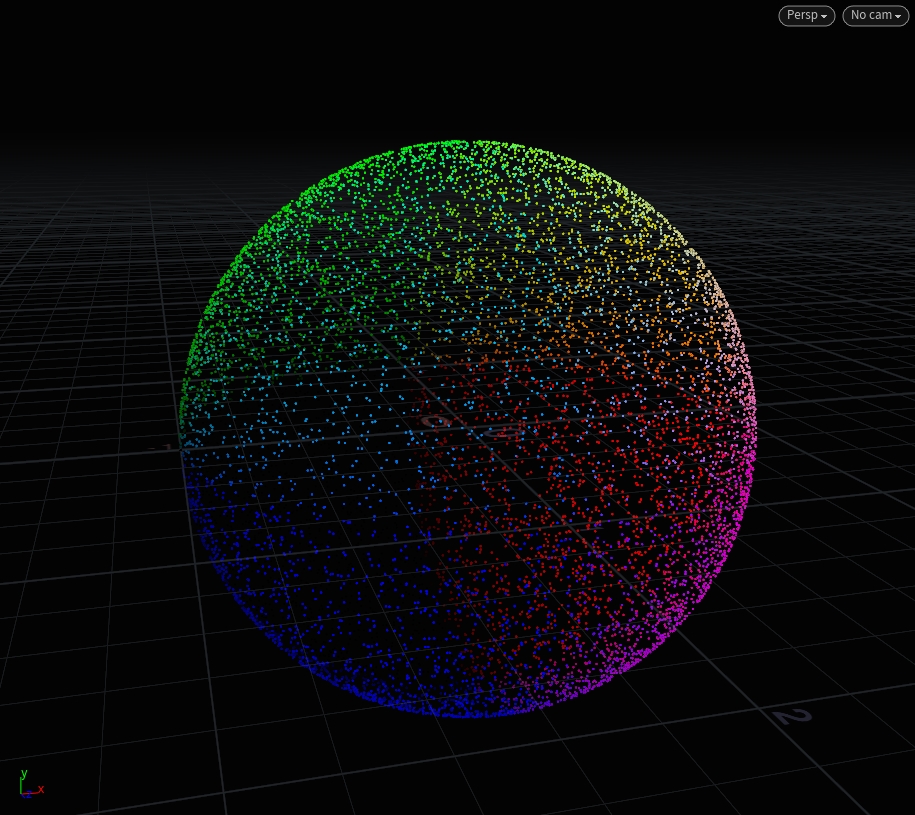
Sample Hemisphere
This function takes a center and a bias. Think of “center” in sample functions as “direction” – so {0, 1, 0} is up, {0, -1, 0} is down – and bias is simply the “angle of spread”.
vector2 uv = rand(@ptnum);
float bias = @Frame;
@P = sample_hemisphere({0, 0, 0}, bias, uv);
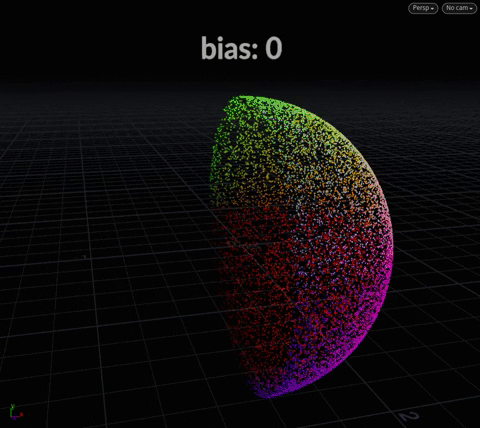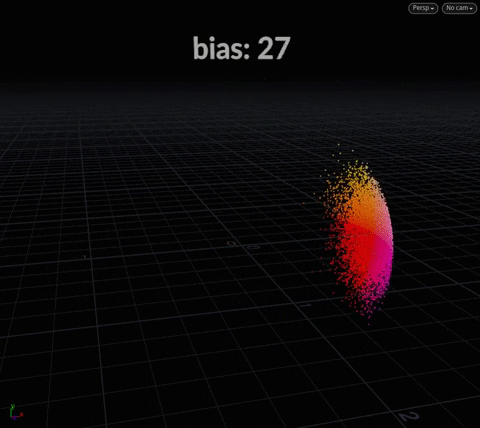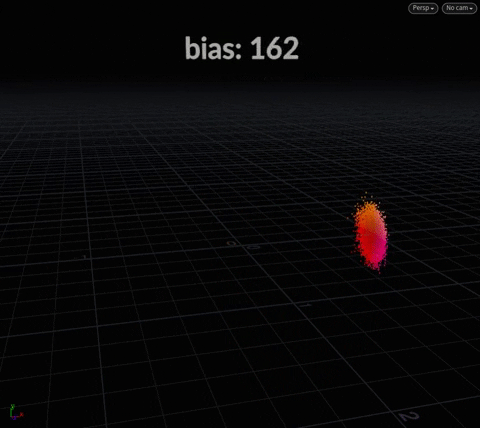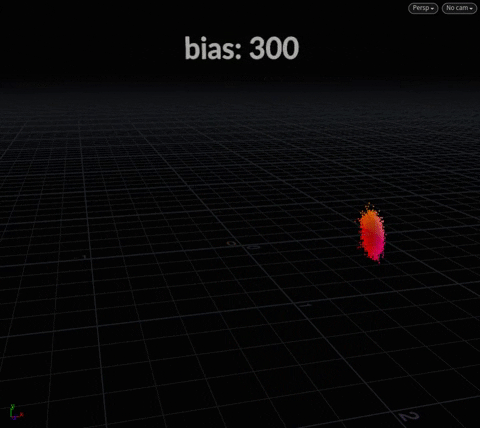
Sample Direction Cone
This is probably the most useful, instead of bias we just use angle instead to achieve something similar. This time, we’ll scatter upwards using {0, 1, 0} as the center.
vector2 uv = rand(@ptnum);
float angle = 90; // the "spread" of the cone @P = sample_direction_cone({0, 1, 0}, radians(angle), uv);

We could imagine using this to shoot out random particles, so instead of @P we could assign it to @v as initial velocity to a DOP – while constraining how far they spread.
But what happens if we want the magnitudes to be the same? Right now, we have some vectors that are ahead of others because it’s a dome-like spread.
We achieve this by only varying v in the uv.
vector2 uv = set(1, rand(@ptnum));
@P = sample_direction_cone({1,0,0}, radians(angle), uv);

Now the values are “clamped” along whichever axis the center is on e.g. all the points have the same @P.x value – since we are scattering in {1, 0, 0}.
Another way of thinking about this, if we have particles getting shot out in +x direction, they can only vary/wiggle up-down (y) or left-right (z) but how far they go (x) is always the same across all points.
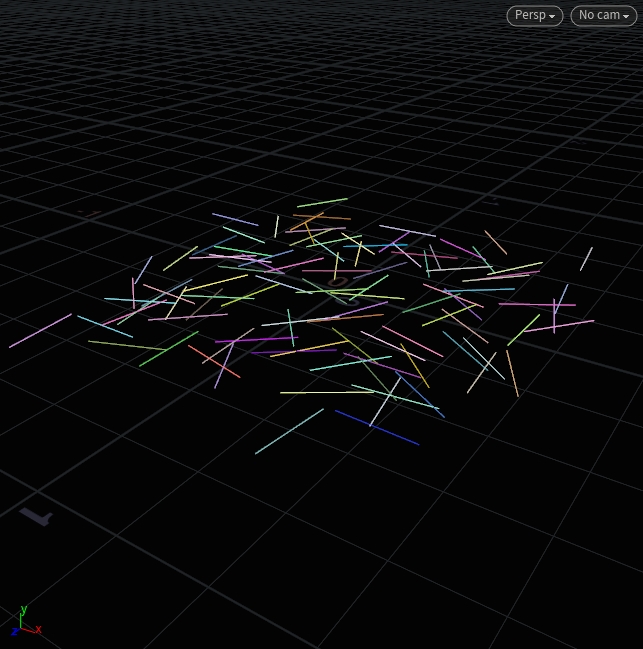
At radians(90) the vectors are perpendicular to the projection plane. We can use this to randomly scatter lines that are perfectly flat on the ground but point in different directions:
// Before a Copy to Points SOP
@N = sample_direction_cone({0, 1, 0}, radians(90), set(1, rand(@ptnum)));
Sample Hypersphere Uniform
This is a quick way to randomly rotate a bunch of girls around in a Copy to Points e.g. get a random @orient.
@orient = sample_hypersphere_uniform(rand(@ptnum));

Links
- The Joy Of VEX
- Pragmatic VEX
Pragmatic VEX series is aimed to increase the technical capacity of the artists and TDs which will allow them to tackle more complex production shots with complete control and ease by acquiring a deeper technical understanding of how things work in Houdini at the lowest level with a strong applied focus on high-end feature film visual effects production. - Get vexed blog
- A collection of code snippets and examples showing syntax and capabilities of VEX