Vector operations

· Mathematics · Vector · Radford Mathematics - Vectors & Matrices · Khan Academy Linear Algebra ·

TOC

• Definition
  • Properties
  • ijk vector representation
  • Vector length
• Vector operations
  • Vector addition
  • Vector subtraction
  • Vector to scalar multiplication (vector result)
  • Dot product (scalar product)
    • Properties
    • Usage
      • Alignment
      • Cosine of the angle
      • Project vector onto a line
      • Project ray onto a plane
      • Shading
  • Cross product (vector product)
    • Properties
    • Cross product to calculate the area of a
  • Angle between vectors
  • A line crossing 2 points
  • Vectors blend (unversal for no unit vectors)

Definition

Vectors are quantities that are defined by two things:

• their magnitude, and
• their direction.

A couple of examples of vectors are velocity and force.
In 2 dimensions, a Vector is described by two components:

• a horizontal component, x component
• a vertical component, y component

Properties

All perpendicular vectors are orthogonal but not vice versa
A zero vector is orthogonal to anything including itself
The (non zero) vectors are collinear if one of them is scalar multiple of the other (same Vector of different length), the angle between collinear vectors is zero

ijk vector representation

as a sum of its components multiplied by the corresponding unit vectors $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$

$\overrightarrow{i}=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),\overrightarrow{j}=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right),\overrightarrow{k}=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$

$\overrightarrow{a}=a_1\overrightarrow{i}+a_2\overrightarrow{j}+a_3\overrightarrow{k}$

Vector length

Vector length is equal to the square root of the sums of its squared coordinates

$\Vert \overrightarrow{a}\Vert =\sqrt{a_1^2+a_2^2+\dots +a_n^2}$

and also follows that

$\Vert \overrightarrow{a}{\Vert }^2=\overrightarrow{a}\cdot \overrightarrow{a}$

Vector operations

Vector addition

$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}=\left(\begin{array}{c}{a}_1+b_2\\ a_2+b_2\\ \dots \\ a_n+b_n\end{array}\right)$

Vector subtraction

$\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})=\left(\begin{array}{c}{a}_1-b_2\\ a_2-b_2\\ \dots \\ a_n-b_n\end{array}\right)$

The resulting vector $\overrightarrow{c}$ 's head is at the vector $\overrightarrow{a}$ 's head

Vector to scalar multiplication (vector result)

$\overrightarrow{c}=b\cdot \overrightarrow{a}\left(\begin{array}{c}b{a}_1\\ b{a}_2\\ \dots \\ b{a}_n\end{array}\right)$

Dot product (scalar product)

Defined for any dimensionality

$\overrightarrow{c}=\overrightarrow{a}\cdot \overrightarrow{b}=\left(\begin{array}{c}{a}_1\\ a_2\\ \dots \\ a_n\end{array}\right)\cdot \left(\begin{array}{c}{b}_1\\ b_2\\ \dots \\ b_n\end{array}\right)=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n$

Properties

• commutative property: $\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{b}\cdot \overrightarrow{a}$

• distributive property: $(\overrightarrow{a}+\overrightarrow{b})\cdot \overrightarrow{c}=\overrightarrow{a}\cdot \overrightarrow{c}+\overrightarrow{b}\cdot \overrightarrow{c}$

• associative property: $(c\cdot \overrightarrow{a})\cdot \overrightarrow{b}=c\cdot (\overrightarrow{a}\cdot \overrightarrow{b})$

• $\overrightarrow{a}\cdot \overrightarrow{a}=\Vert \overrightarrow{a}{\Vert }^2$

• $\overrightarrow{a}$ and $\overrightarrow{b}$ are orthogonal (and perpendicular if not zero) when the dot product $\overrightarrow{a}\cdot \overrightarrow{b}=0$

• law of cosine: $\overrightarrow{a}\cdot \overrightarrow{b}=\Vert \overrightarrow{a}\Vert \cdot \Vert \overrightarrow{b}\Vert \cdot \cos (\varphi )$ where $\varphi$ is the angle between $\overrightarrow{a}$ and $\overrightarrow{b}$

• in geometric sense the dot product gives how much of the vectors are going in the same direction, or a projection (shadow) of one vector on another

Usage

Alignment

With normalized vectors

Cosine of the angle

With normalized vectors

cos(C) * length(a) * length(b) == dtot(a, b); // When not normalized
dot(a, b) > cos(PI, 0.25);                    // check if the angle is less than 45 degrees

Project vector onto a line

float2 P = S + a * dot(a, b);

Project ray onto a plane

float t = -(dot(n, O) + k) / dot (n, d);
P = O + d * t;*

Shading

Fresnel

float fresnel = pow(1.0 - dot(viewDirectionWS, normalWS), 4.0)

Lightweight shading for low-end and mobile, cheaper than the Unity's PBR

// Geometry term
float diffuse = max(0.0, dot(normalWS, lightDirectionWS)) * (1.0 - metalness);

// Specular term
float3 halfwayWS = normalize(lightDirectionWS + viewDirectionWS);
float specular = pow(max(0.0, dot(halfwayWS, normalWS)), lerp(1.0, 64.0, gloss)) * metalness;
specular = sqrt(specular);

// Reflection of ambient light on metallic parts
float fresnel = pow(1.0 - dot(viewDirectionWS, input.normalWS), 3.0);
float3 ambientReflection = ambientColor * specularColor * fresnel * metalness;

// Combine all the lighting
float3 light = 0.0;
light += diffuse * lightColor * basemap; // Geometry term
light += sqrt(specular) * specularColor * lightColor; // Specular term
light += ambientReflection; // Ambient reflection
light += basemap.rgb * ambientColor.rgb * occlusion; // Ambient light

Cross product (vector product)

Defined only for 3D space, order dependent

$\overrightarrow{c}=\overrightarrow{a}\times \overrightarrow{b}=\left(\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_2\end{array}\right)$

Properties

• $\Vert \overrightarrow{a}\times \overrightarrow{b}\Vert =\Vert \overrightarrow{a}\Vert \cdot \Vert \overrightarrow{b}\Vert \cdot \cos (\varphi )$, where $\varphi$ is the angle between the vectors

• triple product: $\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})=\overrightarrow{b}\cdot (\overrightarrow{a}\cdot \overrightarrow{c})-\overrightarrow{c}\cdot (\overrightarrow{a}\cdot \overrightarrow{b})$

• resulting $\overrightarrow{c}$ is orthogonal to $\overrightarrow{a}$ and $\overrightarrow{b}$ (and perpendicular, if is not zero vectors)

• #right_hand_rule: $\overrightarrow{a}$ is the index finger, $\overrightarrow{b}$ is the middle finger, the thumb is the resulting $\overrightarrow{c}$
  

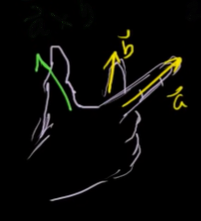
Cross product to calculate the area of a

• parallelogram
  Given the parallelogram with sides of $\overrightarrow{a}$ and $\overrightarrow{b}$, its area is equal to the magnitude of the cross product:

$S=\Vert \overrightarrow{a}\times \overrightarrow{b}\Vert$

• triangle
  Given a triangle whose side are defined by $\overrightarrow{a}$ and $\overrightarrow{b}$, its are is given by:

$S=\frac{\Vert \overrightarrow{a}\times \overrightarrow{b}\Vert }{2}$

The triangle's area is half of the parallelogram's area (see above)

Angle between vectors

Given that $\overrightarrow{a}$ and $\overrightarrow{b}$ are not zero

• if $|\overrightarrow{a}\cdot \overrightarrow{b}|=\Vert \overrightarrow{a}\Vert \cdot \Vert \overrightarrow{b}\Vert$ then $\overrightarrow{a}$ and $\overrightarrow{b}$ are collinear (if non zero vectors), the angle between them is zero, i.e. $\overrightarrow{a}=c\cdot \overrightarrow{b}$

• law of cosine:
  $\overrightarrow{a}\cdot \overrightarrow{b}=\Vert \overrightarrow{a}\Vert \cdot \Vert \overrightarrow{b}\Vert \cdot \cos (\varphi )$
  where $\varphi$ is the angle between the $\overrightarrow{a}$ and $\overrightarrow{b}$, then (?to check?):
  $\varphi =\arccos (\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\Vert \overrightarrow{a}\Vert \cdot \Vert \overrightarrow{b}\Vert })$
  this means that if the vectors are collinear the fraction is = 1 and the arccos(1) = 0 - zero angle between the vectors

A line crossing 2 points

Given 2 position vectors, and parametric $t\in R$ the line $L$ is given by:

$L=\overrightarrow{a}+t(\overrightarrow{a}-\overrightarrow{b})$

the order is not important here, it can be $=\overrightarrow{b}+\dots$ or even $\dots +(\overrightarrow{b}-\overrightarrow{a})$

Vectors blend (unversal for no unit vectors)

Source

Vector3 Slerp(Vector3 start, Vector3 end, float percent)
{
     // Dot product - the cosine of the angle between 2 vectors.
     float dot = Vector3.Dot(start, end);

     // Clamp it to be in the range of Acos()
     // This may be unnecessary, but floating point
     // precision can be a fickle mistress.
     Mathf.Clamp(dot, -1.0f, 1.0f);

     // Acos(dot) returns the angle between start and end,
     // And multiplying that by percent returns the angle between
     // start and the final result.
     float theta = Mathf.Acos(dot) * percent;
     Vector3 RelativeVec = end - start * dot;
     RelativeVec.Normalize();

     // Orthonormal basis
     // The final result.
     return ((start*Mathf.Cos(theta)) + (RelativeVec * Mathf.Sin(theta)));
}